非円柱コロ(Non-cylindrical roller)
(2017.09.06 更新)
コロとは?
コロ(転)とは:重い物を移動させるとき用いる丸棒で、
運ぶ物の下に置き、回転を利用して動かす。

コロの形状は、円柱が常識である。
断面が非円形のコロ
正三角形の各頂点を中心とした円弧で囲まれた「おむすび形」の断面形状を用いると、
断面が円のコロと同じようにコロの上に置かれた物をガタつくことなく運ぶことができる。
(2006.11.14追記)この図形は「ルーローの3角形」と呼ばれているらしい
どんな感じに転がるのかを確認したかったので、ついに作ってしまった


非円柱コロが転がる様子








 非円柱コロが転がる様子のムービー (1.47MB)
非円柱コロが転がる様子のムービー (1.47MB)
非円柱コロの特徴
- 利点1:通常の円柱コロでは、斜面などに置くとコロだけが勝手に転がり去ってしまうことがあるが、
非円柱コロならば、上に物がない状態では安定で転がりにくいため、斜面などに並べておくことが容易である。
- 利点2:地面から上面までの高さを h と置くと、
円柱コロの断面積は πh2 /4 であるが、非円柱コロの断面積は (π−√3)h2/2 である。
h2でくくって係数の項だけで比較すると、π /4 = 0.7853,(π−√3)/2 = 0.7048である。
よって、中身の詰まった(中空ではない)コロを製作した場合、非円柱コロは円柱コロに比べて約90%程度の
材料で済み、10%節約できる。
- 欠点1:上に置かれた物を一定速度で運ぶ場合、非円柱コロの速度や角速度・重心の移動などが一定ではないため、
高速で移動させるのに不向きである。(音や振動が発生してしまう)
- 欠点2:非円柱コロの尖った箇所は線で接触するため、床や運ぶ物体の底面が柔らかい場合には食いに込んでしまって
なめらかな転がりに支障をきたす。
(2011.03.07 追記)欠点2の「尖った箇所」については、以下のようにルーローの3角形を拡張した図形を
用いることによって解消できる。
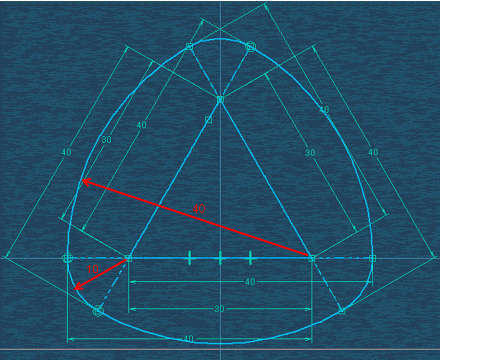
ルーローの3角形が転がらない斜面の最大角度の求め方について
(2017.09.05)
断面がルーローの3角形であるようなコロは、斜面に置いても勝手に転がらない利点があるが、
転がらないで静止可能な斜面の最大角度について検討する。
まず、ルーローの3角形が転がったときの重心の軌跡について考える。
「転がらない」=重心の軌跡カーブの底になる姿勢がある(軌跡カーブの微分=0になる点がある)
ということである。上記の条件を満たす場合、
「転がらない斜面の最大角度」=重心の軌跡カーブの傾きの最大値
である。重心の軌跡カーブの傾きが最大になるのは、ルーローの3角形の正三角形の辺が鉛直になった状態で、
このとき地面との接触点と重心を結ぶ線は鉛直線に対し30度傾く。
すなわちルーローの3角形が転がらない斜面の最大角度=30度である。
頂点の部分が丸くなっている上記の「ルーローの3角形を拡張した図形」が転がらない斜面の最大角度の求め方も同様で、
重心の軌跡カーブの傾きが最大になるのは、ルーローの3角形の正三角形の辺が鉛直になった状態である。
このとき、地面との接触点と重心を結ぶ線と鉛直線との角度、すなわち転がらない斜面の最大角度は
必ず30度以下になる。
非円柱コロの拡張
正三角錐(正四面体)の角頂点を中心とした球面で囲まれる立体も同じような性質を示すことが
予想される。しかしながらこの場合、頂点部分は点接触となるため実用上は使い物にならないだろう。
このような立体は「ルーローの四面体」と呼ばれるそうですが、
ルーローの三角形ほど話は単純ではないようです。
それは、上面と下面で接する部分が頂点と球面だけとは限らず、辺の部分同士で接することがあり、
その場合定幅とはならないとのことです。
大変おもしろい記述のあるサイトを見つけましたので、
無断でリンクさせていただきました。
「準ルーロ−4面体」のページのサイトへ
(2010.09.19 追記)ニュートン別冊の図形に関する雑誌を本屋で立ち読みしていたところ、
ルーローの3角形を3次元に拡張する議論が掲載されていて、その1つの解答として、
ルーローの3角形を軸対称図形と考えたときの軸を中心にして回転させた立体が
定幅立体(等幅立体かも)になるとの記述があった。軸対象でドングリのような形で、
個人的にはあまり好みの立体ではないが、
一応CADで作図してみたのでここに挙げておく。
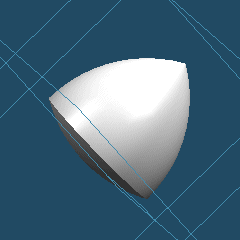

「定幅立体」の立体データ(STL形式,865KB)ルーローの3角形の基本となる3角形の1辺は50mmで作図
そのうち機械で削ったりして実物を作って実験するかも
【参考文献】ニュートンムック Newton別冊 図形に強くなる--―「カタチ」をめぐる数学の不思議,
ニュ−トンプレス, 2010年8月発行
ご意見・ご感想・お問い合わせは下記までe-mailにてお願いします:
もどる