連続な多次元変数の最適化:実数値遺伝的アルゴリズム
世代交代モデルJGG + 多親交叉REX
遺伝的アルゴリズム(Genetic Algorithms: GA)は、その枠組みのシンプルさと
特に高次元の多次元変数を持つ最適化問題における探索性能の高さ、
多目的最適化問題への対応など、実問題の要求に答えることができる最適化手法として
広く認知されています。特に連続パラメータをビット列の遺伝子に直さずにそのまま用いる
Real-coded GA (RGA) はかなり強力な手法として多くの実問題に用いられています。
本ページでは、実数値GAの一種であるJGG+REXのJavaプログラムを
公開しています。JGG(Just Generation Gap) +REX(Real-Coded Ensemble Crossover) は、東京工業大学教授の小林重信先生がご提案された
世代交代モデルJGGと多親交叉REXを組み合わせた実数値GAで、
アルゴリズムが単純で実装が簡単な割に探索能力が強力です。
(2011.12.20)実数値GAの交叉オペレーションREXは、参考論文ではかなりのパフォーマンスを示していますが、
その後の論文等によると変数依存性の強い問題(例えばローゼンブロック関数など)では正規分布交叉(UNDX)よりも
性能が劣るという報告がありました。
(参考文献)
秋本 洋平, 永田 裕一, 佐久間 淳, 小野 功, 小林 重信:
実数値GAにおける生存選択モデルとしてのMGGとJGGの挙動解析,
人工知能学会論文誌, Vol. 25 (2010) , No. 2, pp.281-289.
2011年12月の時点で私が知る限り、最強の実数値GAは CMA-ES と呼ばれるアルゴリズムです。
以下のサイトにCやFortran, Javaなど様々な言語で書かれたコードがあります:
http://www.lri.fr/~hansen/
ちなみにJGGのJは「just」となっていますが、世代交代モデルMGGのMと、
NSGA2で有名なDeb氏の提案した世代交代モデルGGGのGのちょうど中間がJだったので、
Jで始まる適当な単語を探してJustになったとか。宴席で伺った話なのでどこまでが本当かネタか分かりませんが
以下に実数値GAのJGG+REXについて説明した資料を挙げます:
PDFファイル RGA_JGG_REX.pdf
【参考文献】小林重信:実数値GAのフロンティア
人工知能学会論文誌Vol.24, No.1, pp.147--162, 2009.
(英文表記)Shigenobu Kobayashi: The Frontiers of Real-Coded Genetic Algorithms,
Transactions of the Japanese Society for Artificial Intelligence,
Vol.24, No.1, pp.147--162, 2009.
この文献は
人工知能学会のWEBサイト(正確にはJ-STAGE)より無料でダウンロードできます。
九州大学にて開催された小林先生の進化計算に関する講演会にて、
参考となる資料が公開されましたので挙げておきます:
計測自動制御学会九州支部 第14回講義会
実数値GA(JGG+REX)のJavaプログラム
最適化を行おうとする研究者やエンジニアには様々な方がおられますので、
使用する言語もいろいろです。
情報工学や制御工学等ではCやC++言語が標準的ですが、
当部門(船舶海洋システム工学部門)のように流体や構造を専門にする場合はFortranを標準的に使用しておりますし、
アプリケーションソフトの開発現場ではマイクロソフト社のVB/VBAだったりします。
ネットワークプログラムを組む場合は、Java言語がよく使われます。
Javaは携帯アプリなどにも使用されています。
ここでは実数値GA(JGG+REX)のJavaプログラムを公開しますが、
目的関数(コスト関数)のプログラムは使う人がそれぞれに組む必要があります。
どんな言語でも使えるようにするため、滑降シンプレックス法のプログラムと
目的関数(コスト関数)のプログラムをそれぞれ独立した別々のプロセスとして
走らせて、ファイルシステムを介してデータのやりとりを行うような仕様としました。
これにより、例えば流体抵抗の計算プログラムがFortranで書かれていても、
ファイル入出力によってJavaプログラムと通信を行って最適化が行えるようになります。
さらにファイルシステムにNFS(network file system: Windowsでは外部から読み書きできる共有フォルダ)
を利用すれば、探索アルゴリズムの走る計算機とパラメータのコスト関数を計算する計算機を
別々にすることも可能です。
実数値GA(JGG+REX)のJavaソースプログラムとコンパイル済みクラスファイル
本プログラムの著作権は作者が所有しますが、プログラムの改変などは自由です。
本プログラムを使用したことによって生じたいかなる損害に対しても著作権保有者は責任を負いません。
各自の責任のもとで実行してください。
プログラムのバグなど発見された場合は、ぜひお知らせください。
- 実数値GA(JGG+REX)のJavaソースファイルとクラスファイル(コスト計算プログラムのサンプル付き)
RGA_REXandJGG_usingFileSystem.zip
- コスト計算プログラムのサンプルのJavaソースファイルとクラスファイル
ObjectiveFunctionSampleProgram.zip
ローゼンブロック関数(単純なプログラム)
ObjectiveFuncMultiLinkArm.zip
マルチリンクアーム問題(Windowアプリケーション)
実数値GA(JGG+REX)のJavaプログラムの使い方
上記の RGA_REXandJGG_usingFileSystem.zip
をダウンロードして展開すると、以下のファイル群が出てきます:
- RGA_REX_JGG.class, SMPINDV.class ← 実数値GA(JGG+REX)のクラス
- RGA_REX_JGG.java ← 実数値GA(JGG+REX)クラスのソースプログラム
- FitnessFuncByFile.class
- FitnessFuncByFile.java
- FitnessFunction.class ← FitnessFunctionの基本クラス
- FitnessFunction.java ← FitnessFunction基本クラスのソース
- FunctionOptimization.class ← 実行するプログラム本体
- FunctionOptimization.java
- 集団数300親12子100で探索.bat ← プログラム本体を起動するバッチファイルの例
- MT19937.class ← 乱数発生クラス(メルセンヌツイスター)
- MT19937.java
- RGA_REX_JGG.html ← プログラムの使い方についての説明
- RGA_REX_JGG.pdf ← 実数値GA(JGG+REX)についての説明資料
- feature.gif ← プログラム間の通信仕様についての図
- config.txt, param.txt, result.txt ← (後述)
- Rosenbrock.class ←20次元ローゼンブロック問題のクラス
- Rosenbrock.java ←20次元ローゼンブロック問題クラスのソースプログラム
- 20次元ローゼンブロック問題を起動する.bat ←起動バッチファイル
- MultiJointArm.class, CostFuncRoboWin.class, PLANT_F_Canvas.class ←マルチリンクアーム問題のクラス
- マルチリンクアーム問題10関節で起動.bat ←マルチリンクアーム問題プログラムを起動するバッチファイル
実行するには JDK1.4以降のJava実行環境が必要です。
本プログラムは version 1.5.0_06 にて動作を確認しています。
【注意】このプログラムを実行する前に、後述のコスト計算プログラムを予め走らせておく必要があります
実数値GA(JGG+REX)プログラムを実行するには、コマンドプロンプト上(通称DOS窓)において
CDコマンドによりプログラムの存在するフォルダまで移動した後、後で説明する config.txt があることを確認して、
以下のような例でコマンドを実行します:
> java FunctionOptimization 10000 300 12 100
ここで第一引数 10000 は、探索を行う回数(コスト関数の評価回数)の上限を与えます。
値を大きくするといつまでも探索を続けます。
第2引数の 300 は集団個体数、,Br>
第3引数の 12 は世代交代JGGにおける多親個体数、
第4引数の 100 は世代交代JGGにおける子個体生成数を与えます。
バッチファイル「集団数300親12子100で探索.bat」をダブルクリックすると、
上記コマンドを実行してくれます。
コスト計算のサンプルプログラムの使い方
上記の RGA_REXandJGG_usingFileSystem.zip
の中に2種類のコスト計算プログラムのサンプルが入っており、以下が該当します:
- Rosenbrock.class ←20次元ローゼンブロック問題のクラス
- Rosenbrock.java ←20次元ローゼンブロック問題クラスのソースプログラム
- 20次元ローゼンブロック問題を起動する.bat ←起動バッチファイル
- MultiJointArm.class, CostFuncRoboWin.class, PLANT_F_Canvas.class ←マルチリンクアーム問題のクラス
- マルチリンクアーム問題10関節で起動.bat ←マルチリンクアーム問題プログラムを起動するバッチファイル
バッチファイルをダブルクリックすれば起動します。
【注意】コスト計算プログラムは、実数値GAプログラムを実行する前に予め走らせておく必要があります。
それぞれの例題のソースプログラム等は以下からダウンロードしてください:
ObjectiveFunctionSampleProgram.zip
ローゼンブロック関数のソースプログラム等
ObjectiveFuncMultiLinkArm.zip.zip
マルチリンクアーム問題のソースプログラム等
これらのプログラムは、実数値GAプログラムが走っているのと同じフォルダへコピーして実行する必要があります。
実数値GA(JGG+REX)プログラムとコスト計算プログラムを別々のプロセスで走らせるには?
WindowsXPのパソコンであれば、DOS窓を2つ開いて、CDコマンドで同じそれぞれ同じフォルダへ移動して
片方で滑降シンプレックス法プログラムを実行し、もう片方でコスト計算プログラムを実行します。
デスクトップはこんな感じになります
WindowsXPのデスクトップ上でコマンドプロンプト(DOS窓)を2つ開いた状態
Windowsの共有フォルダを使えば、実数値GAプログラムとコスト計算プログラムを別々のパソコン上で
実行できるのですが、実数値GAはカレントのフォルダのファイルのみを読み書きするので、
コスト計算プログラムのほうを共有フォルダのファイルの読み書きできるよう修正してください。
実数値GA(JGG+REX)プログラムの通信仕様
Java以外の言語でコスト計算プログラム作る場合、
以下のようなファイルのやりとりによって計算するように作る必要があります。
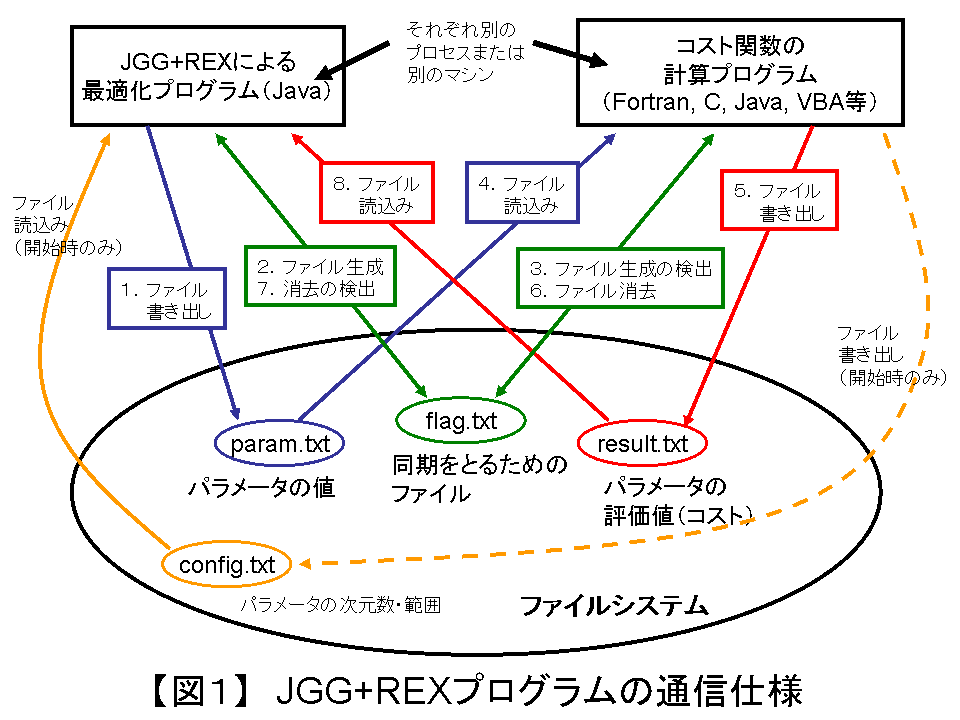
【初期設定】
・まず、解くべき問題のパラメータ数と、パラメータの定義域について指示するため、
config.txt ファイルにそれらを書き込んでおきます。
・実数値GAプログラムは config.txt ファイルを読み込んで初期設定を行います。
【最適化のための通信】
・初期設定が終了したら、以下のやりとりを繰り返します:
- 実数値GAプログラムは、コスト計算プログラムに計算すべきパラメータの値を渡すため、
param.txt ファイルへパラメータの値を書き込みます
- 実数値GAプログラムは、コスト計算プログラムに param.txt ファイルが用意できたことを
通知するために flag.txt ファイルを生成します。
- コスト計算プログラムは、flag.txt ファイルが生成されるまで待ちます。
- コスト計算プログラムは、flag.txt ファイルが生成されたことを確認したら
param.txt ファイルを開いてパラメータの値を読み込み、コストを計算します。
- コスト計算プログラムは、計算結果を result.txt へ書き込みます。
- コスト計算プログラムは、計算終了を実数値GAプログラムへ通知するために
flag.txt ファイルを消去します。
- 実数値GAプログラムは、flag.txt ファイルが消去されるまで待ちます。
- 実数値GAプログラムは、flag.txt ファイルの消滅を確認したら、
result.txt を読み込みます。
以上の処理を所定の回数繰り返して最適化を行います。
所定の回数を繰り返したら、実数値GAプログラムは、
コスト計算プログラムに計算終了を通知するため end.txt ファイルを生成して処理を終了します。
【config.txt ファイルの仕様】
解くべき問題のパラメータ数と、パラメータの定義域について指示します。
(ただし、この定義域は、初期解の生成のみに使用しています。探索中にこの領域外へ出ることがあります。)
先頭行において、文字列「NumOfParameters」と空白文字に続いて、パラメータの個数を書きます。
2行目以降は文字列「ParamRangeMin」と空白文字に続いてパラメータの定義域の下界の数値、
さらに空白文字に続いて文字列「ParamRangeMax」と空白文字に続いてパラメータの定義域の上界の数値を書きます。
この行はパラメータの個数分なければなりません。
(4次元のパラメータの最適化を指示するための config.txt ファイルの例)
NumOfParameters 4
ParamRangeMin -5 ParamRangeMax 5
ParamRangeMin -5 ParamRangeMax 5
ParamRangeMin -5 ParamRangeMax 5
ParamRangeMin -5 ParamRangeMax 5
【param.txt ファイルの仕様】
param.txt にはパラメータの数値がスペースで区切られて書き込まれます。
(4次元のパラメータを表すための param.txt ファイルの例)
1.1 1.2 0.4 0.3
【result.txt ファイルの仕様】
result.txt には、cost という文字列に続いて評価値の数値を書き込みます。
小さい値ほど良い評価であるものとします。
(result.txtファイルの例)
cost 20
【flag.txt および end.txt ファイルの仕様】
これらはファイルの有無だけが問題なので、
ファイルの中身は空です。
最近のWindowsXPを積んだパソコンは、複数のプロセスを走らせることが簡単なので、
このような方法はエレガントではありませんが簡単でなかなか便利です。
本プログラムの代わりに、 滑降シンプレックス法のプログラム(Java) や
共役勾配法のプログラム(Java)
などを同じように走らせれば、全くプログラムの変更をせずに別の手法で最適化できます。
ご意見・お問い合わせ等は以下のURLにメールアドレス等がありますので、
そちらからお願いします:
http://sysplan.nams.kyushu-u.ac.jp/gen/index.html
九州大学 大学院工学研究院 海洋システム工学部門 木村 元
