配管および機器配置の自動設計システムに関する研究

2点間を結ぶ配管経路探索アルゴリズム

設計対象の空間を等間隔メッシュに分割し、 配管経路探索アルゴリズムにダイクストラ法を適用することで最適な経路を探索するアプローチが 多数提案されている (1) 。 ダイクストラ法とは、 グラフ上の２ノード間の最短経路を効率良く求めるアルゴリズムである。

【第１図】７個のノードと11本の重み付き辺から構成されたグラフの例　矢印はＳからＧへの最短経路

グラフとは、第１図に示すように円で表されるノードとそれらを結ぶ辺で表されるネットワークで、 各辺には正のコストが付与される。 このアプローチは、設計対象をメッシュ分割する際、 各メッシュ毎に異なるコストを設定することにより、 作業員用の通路を避けつつ壁際やパイプラックにパイプを配置可能になるなどの優れた特徴を有している。

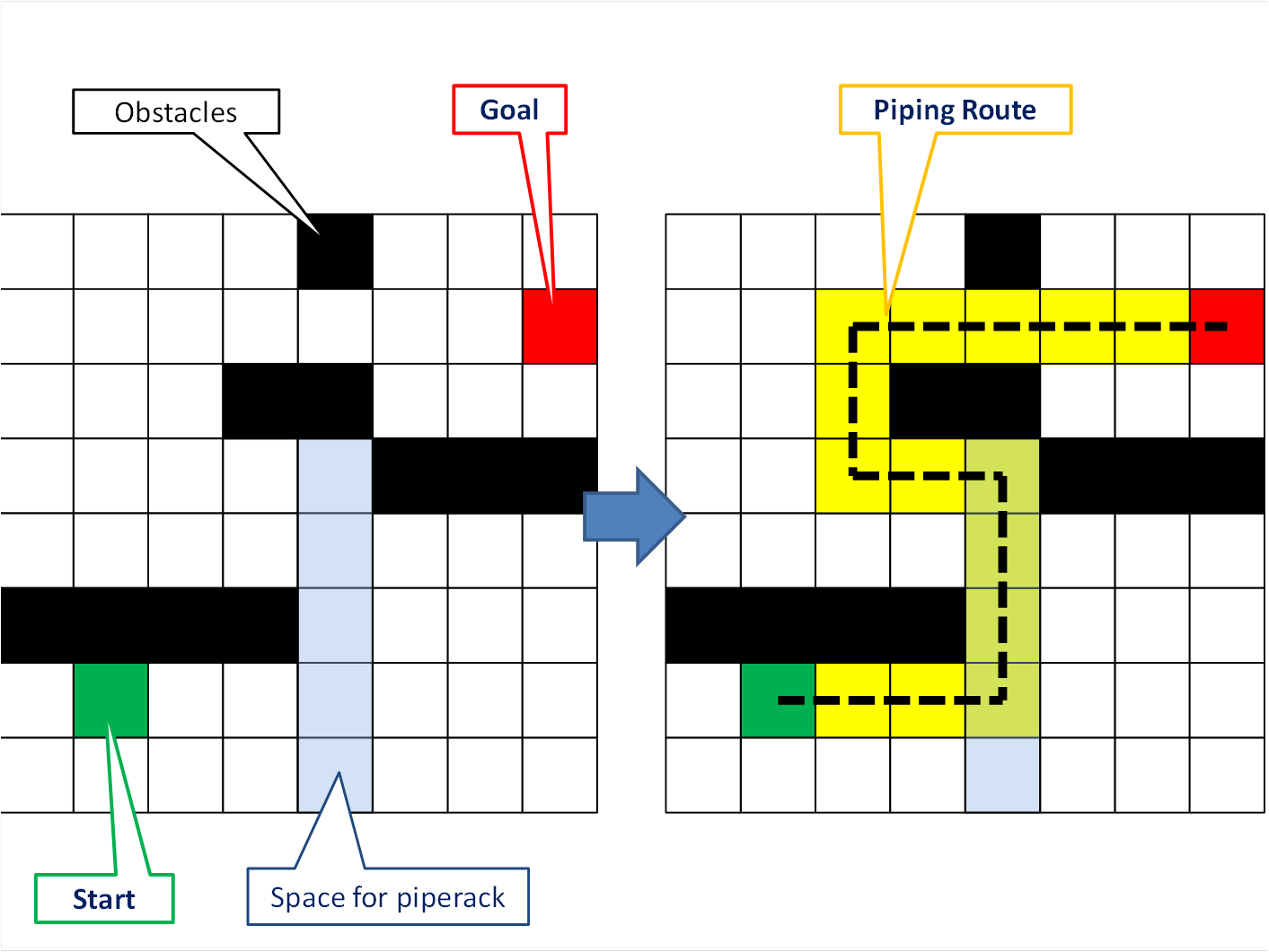
【第２図】設計対象空間を管径以上のメッシュに分割してダイクストラ法によって最短経路を得る例

しかし、ダイクストラ法を用いる配管設計法では、 第２図のように設計対象の空間を必ずパイプ径以上の等間隔メッシュで分割し、 配管経路を直管とエルボのみで構成するのが一般的であった。 そのためパイプの始点や終点を構成する機器や障害物などの位置や寸法に大きな制約が課せられ、 さらに設計対象空間に比して比較的径の大きな管などＳ字状のベンドを多用しなければならない状況には対処不能などの問題があり非実用的だった。 著者らは、設計対象の空間をパイプ直径に依存しない自由な寸法でメッシュ分割する方法 (2) (3) を提案した。 これは、設計対象空間を格子状に分割して重み付きグラフを生成する際、 グラフのノードを特徴付ける状態量として、 格子分割した各格子の位置座標に加え、 その格子を通るパイプの方向を考慮するものである。

【第３図】管径に依存しない格子分割による2次元空間での直管およびエルボ配置のグラフ表現

第３図は、２次元空間での配管設計における上記の新手法による空間分割方法および直管とエルボを用いた配管部分を グラフで表した例である。

【第４図】Ｓ字状のベンド管ピース

また、管径以下のずれ dが存在する直管同士を接続する場合、 第４図のようにＳ字状に曲がったベンド管が使用され、 ベンドの工作上の制約から決まる曲げ半径係数α1,α2よりベンド設置に必要な最小距離L が求められる。 これより、Ｓ字状のベンドを使用した場合のグラフ表現は第５図のように与えられる。

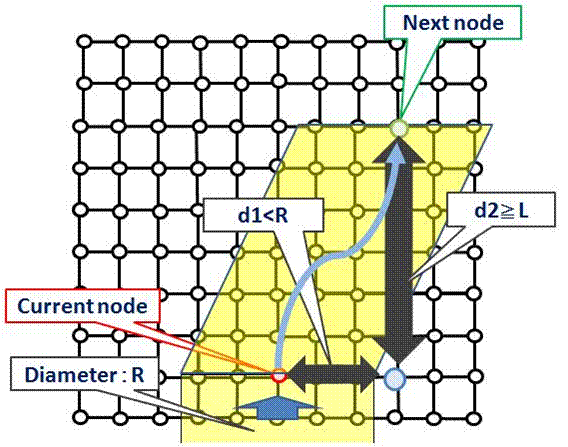
【第５図】管径に依存しない格子分割による2次元空間でＳ字状ベンド配置のグラフ表現

以上より、管径に依存しない格子上に直管・エルボ・Ｓ字状のベンドといったパイプピースを配置する配管経路設計問題は、 各ピースを辺とした重み付きグラフとして表現され、 既存の経路探索法を用いて最適解を得ることができる。

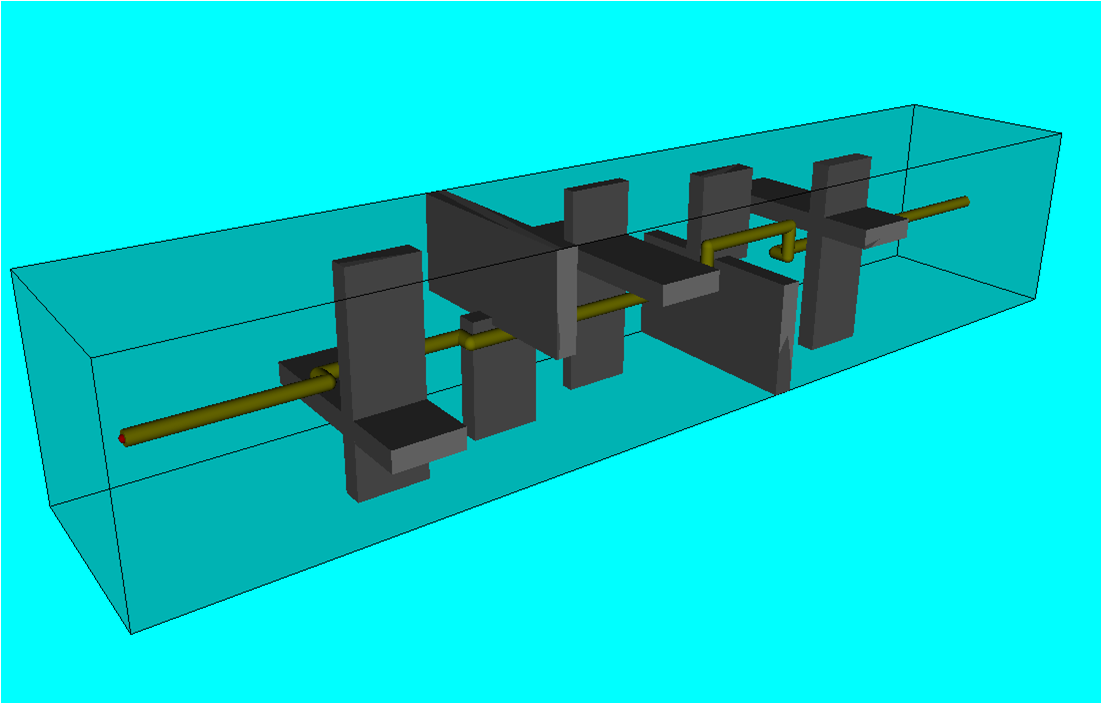
【第６図】φ200のパイプにおける自動配管設計で得られた経路


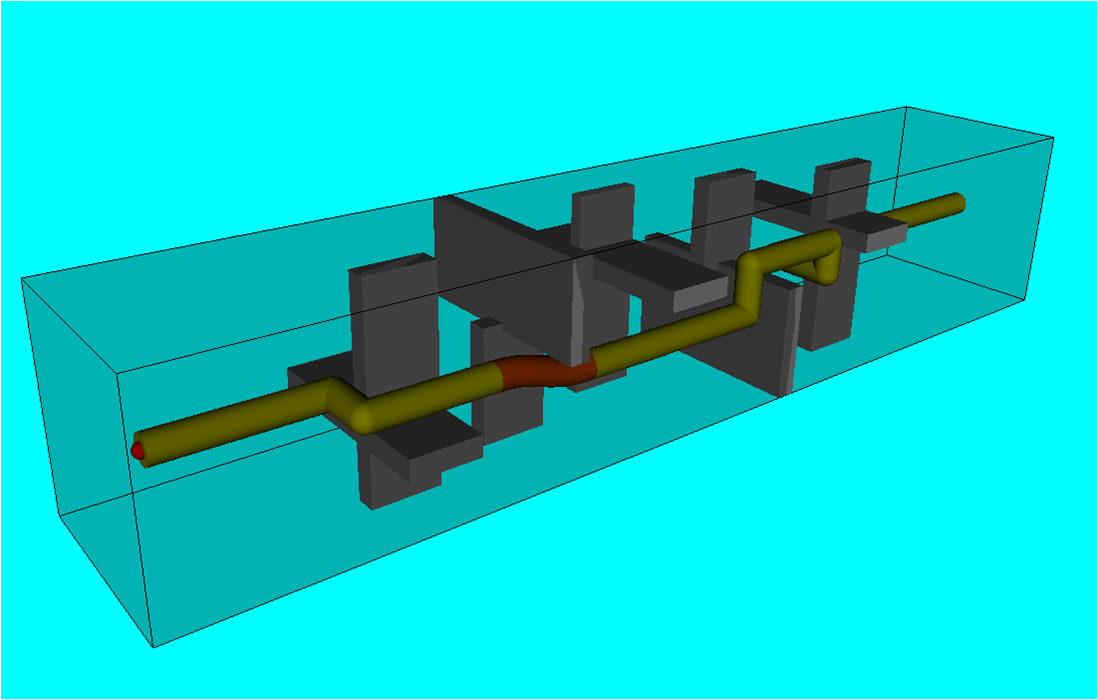
【第７図】φ400のパイプにおける自動配管設計で得られた経路


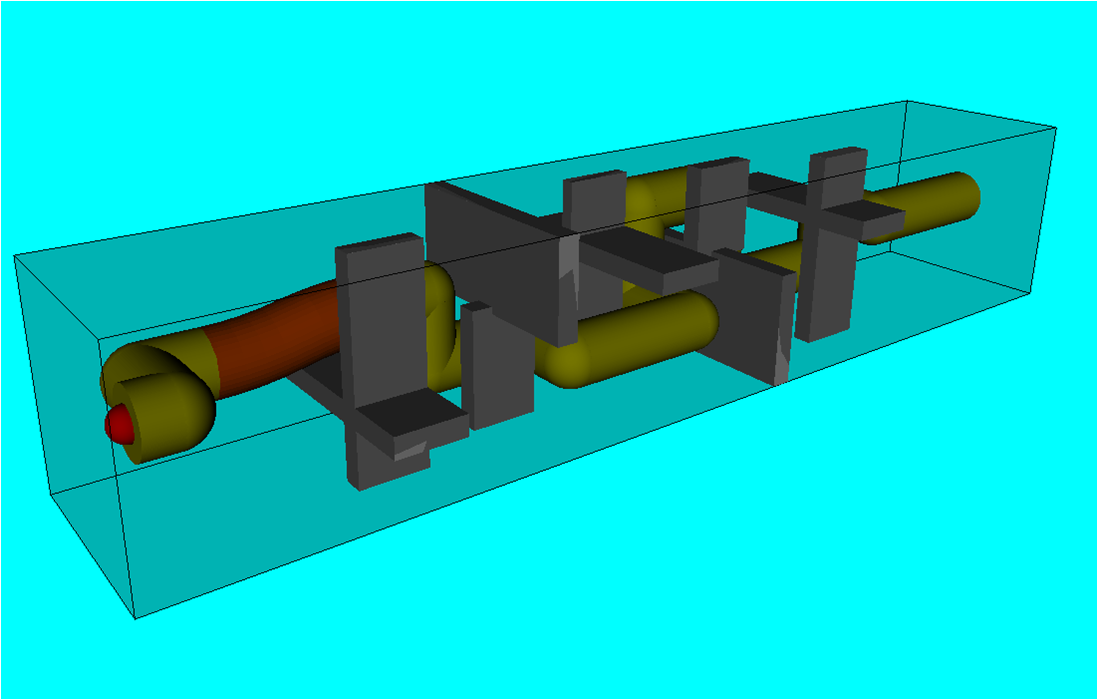
【第８図】φ900のパイプにおける自動配管設計で得られた経路

第６，第７，第８図は、 幅3[m]高さ3[m]奥行16[m]の空間に10個の直方体の障害物を配置し、 空間を250[mm]の等間隔格子に分割して上記の新しい経路探索法を適用して得た配管経路である。 第６，第７，第８図全てにおいて障害物の位置とパイプの始点および終点座標は同一であるが、 管径がそれぞれ異なる。標準的なMS-Windows搭載のPC上で計算した場合、 管径が太い場合は数秒、管径が細い場合はネットワーク構造が大きくなる関係で数分を要する。 径が小さい場合は障害物の回避が簡単なのでほぼ直線状の経路が得られているのに対し、 径が大きいと障害物回避が難しいため遠回りになり、 さらにベンドを用いる複雑な経路が最小コストの経路となっている。 このような最適経路をハンドコーディングで得ることは困難であり、 自動計算が実用的なものであることを実証した。

＜参考文献＞

＜自動配管プログラムのダウンロード＞

• プログラムの使用方法・入力データの仕様等の説明
  
• Javaプログラム等一式（AutomaticRouting20130520.zip, 0.98MB）