迷路問題をQ-learningで学習する

状態遷移に不確実性がない場合

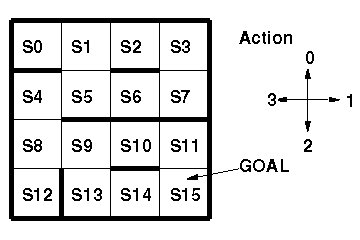
以下のように，ラベル付けされた現在位置を状態として観測可能な迷路がある。 各意思決定において４種類の行動のうちどれか１つを実行すると， その行動に応じた状態遷移を行う。 ゴールに到達すると正の報酬が与えられ，ゴール状態で行動を実行すると 無条件でS0へジャンプする。(下図を参照)

よって，獲得報酬を最大化するような制御規則（状態→行動への写像）は， ゴールへ最短パスで到達する制御規則となる。

以下に迷路問題をQ-learningで解くアプレットを示す。
Discount rateは割引率，Learning rateは学習率を表す。 行動選択戦略としてε-greedy戦略をとる。これらの値はスクロールバー によって調節可能である。
[Run]ボタンを押すと学習を開始する。

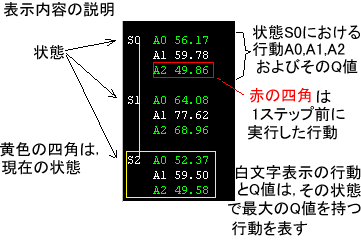
Q-learningエージェントの表示について以下に説明する。

Q-learningアルゴリズムの詳細は 3.3 マルコフ決定過程(MDP)の環境における強化学習(Q-learning)を参照。

Q値の学習と最適な行動の獲得について

十分に時間が経過して，正しくQ値の推定学習がなされた場合， 最大のQ値を持つ行動が最適な行動となる。 このとき，ε-greedy行動選択戦略においてε=0とすれば， エージェントは最適な行動を実行する。

この迷路問題では，状態遷移に不確実性がないため，学習率（Learning rate) = 1.0 にすると 最も高速に学習できる。
しかし，この問題のように「状態遷移に不確実性がない」場合には，強化学習アルゴリズムよりも 他のサーチアルゴリズム等を用いた方がずっと効率よく学習可能であることは明らかである。
ここで強調したいのは，決定的な遷移をする迷路問題だけでなく，一見迷路問題とは全く異質な タクシー問題等の不確実な遷移を伴う問題も，強化学習によって区別なく扱えるという点である。 しかし，異質な問題間では学習率などのパラメータの適切な値はかなり異なってくる。