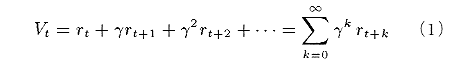
ただし rt は時刻 t における報酬である. この Vt の期待値は,1 ステップあたり ( 1 - γ ) の確率で停止するエージェ ントによって得られる報酬合計の期待値と等価である. 未来の報酬を割引く理由は以下による.
本ページの記述は下記の解説記事をもとにWEB用に修正したものである:
木村 元,宮崎 和光,小林 重信:
強化学習システムの設計指針,
計測と制御, Vol.38, No.10, pp.618--623 (1999), 計測自動制御学会.
6 pages, postscript file, sice99.ps (1.31MB)
PDF file, sice99.pdf (148KB)
強化学習とは,試行錯誤を通じて環境に適応する学習制御の枠組である.
教師付き学習(Supervised learning)とは異なり,状態入力に対する正しい行動
出力を明示的に示す教師が存在しない.かわりに報酬というスカラーの情報を
手がかりに学習するが,報酬にはノイズや遅れがある.そのため,
行動を実行した直後の報酬をみるだけでは,学習主体はその行動が正しかっ
たかどうかを判断できないという困難を伴う.
強化学習の枠組をFig.1に示す.
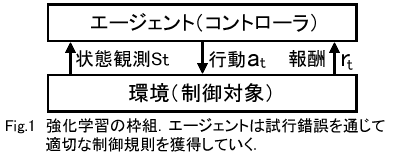
学習主体「エ-ジェント」と制御対象「環境」は以下のやりとりを行う.
エ-ジェントは利得(return: 最も単純な場合,報酬の総計)
の最大化を目的として,状態観測から行動出力へのマッピング(政策(policy)
と呼ばれる)を獲得する.
環境とエ-ジェントには一般に下記の性質が想定される.
強化学習が注目を集める理由の一つは, 不確実性のある環境を扱っている点にある. 多くの実世界の制御問題では,不確実性の扱いは厄介である. もう一つの理由は, 報酬に遅れが存在し,離散的な状態遷移も含んだ段取り的な 制御規則の獲得を行う点にある. 設計者がゴ-ル状態で報酬を与えるという形で, させたいタスクをエ-ジェントに指示しておけば, ゴ-ルへの到達方法はエ-ジェントの試行錯誤学習によって自動的に 獲得される. つまり 設計者が「何をすべきか」をエ-ジェントに報酬という形で 指示しておけば「どのように実現するか」をエ-ジェントが学習によって 自動的に獲得する枠組となっている.
環境に不確実性や計測不能な未知のパラメータが存在すると,タスクの達成方法 やゴールへの到達方法は設計者にとって自明ではない. よってロボットへタスクを遂行するための制御規則をプログラムすることは設計 者にとって重労働である. ところが, 達成すべき目標を報酬によって指示するこ とは前記に比べれば遥かに簡単である. そのため,タスク遂行のためのプログラミングを強化学習で自動化することによ り,設計者の負担軽減が期待できる. 十分に優れた性能を持つ強化学習エージェントをコントローラとして1つだけ開 発しておけば,あとはロボットの目的に応じて報酬の与え方だけを設計者が設定 するだけで,あらゆる種類のロボット制御方法を同一のコントローラによって自 動的に獲得できる.
試行錯誤を通じて学習するため, 人間のエキスパートが得た解よりも優れた解を発見する可能性がある. 特に不確実性(摩擦やガタ,振動,誤差など)や 計測が困難な未知パラメータが多い場合,人間の常識では対処し切れないことが 予想され,強化学習の効果が期待できる. エキスパートの制御規則を学習初期状態に設定して,それを改善する場合 と,全くのゼロから学習を開始し,設計者にとっては意外な新しい解を 発見する場合とが考えられる.
機械故障などの急激な変化やプラントの経年変化のような緩慢な変化など, 予め事態を想定してプログラミングしておくことが困難な環境の変化に対 しても自動的に追従することが期待できる. 特に宇宙や海底など,通信が物理的に困難な場合や, 通信ネットワークの制御のように現象のダイナミクスが人間にとって速すぎる 場合において,強化学習の自律的な適応能力が特に威力を発揮する.
環境のダイナミクスを以下のようにモデル化したのがMDPである.
環境のとりうる状態の集合を S = { s 1 , s 2 , … , s n },
エージェントがとりうる行動の集合を
A = { a 1 , a 2 , … , a l }
と表す.
環境中のある状態 s ∈ S において,エージェントがある行動 a を
実行すると,環境は確率的に状態 s' ∈ S へ遷移する.
その遷移確率を Pr{ st+1 = s' | st = s, at = a }=
Pa(s,s') により表す.
このとき環境からエージェントへ報酬 r が確率的に与えられるが,
その期待値を
E{ rt | st = s, at = a, st+1 = s' }=
Ra(s,s') により表す.
エージェントの各時刻における意志決定は,
政策関数π(s, a) = Pr{ at = a | st = s},
(ただし全状態s,全行動aにおいて定義される)によって表される.
これは単に政策π とも呼ばれる.
●マルコフ性: 状態s'への遷移が, そのときの状態sと行動aにのみ依存し, それ以前の状態や行動には関係ないこと.
●エルゴ-ト性: 任意の状態sからスタ-トし,無限時間経過した後の状態分布確率は 最初の状態とは無関係になること.
ある時間ステップで実行した行動が,
その後の報酬獲得にどの程度貢献したのかを評価するため,
その後得られる報酬の時系列を考える.
報酬の時系列評価は利得(return)と呼ばれる.
エージェントの学習目標は,利得を最大化すること,
あるいはそのような政策を求めることである.
強化学習では,割引報酬合計による評価を利得として用いる場合が多い.
これは,時間の経過とともに報酬を割引率 γ (0 ≦ γ < 1)で割引いて合計する.
ある時刻 tにおける状態,あるいはそのとき実行した行動の利得 V t
を以下で定義する.
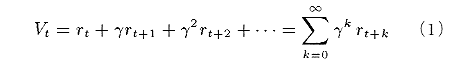
ただし rt は時刻 t における報酬である.
この Vt の期待値は,1 ステップあたり ( 1 - γ ) の確率で停止するエージェ
ントによって得られる報酬合計の期待値と等価である.
未来の報酬を割引く理由は以下による.
●最適なState-Value関数:全ての状態 s において
Vπ(s) ≧ Vπ'(s) となるとき,
政策 π は π' より優れているという.
マルコフ決定過程では,他のどんな政策よりも優れた,あるいは同等な政策が少なくとも1つ存在する.
これを 最適政策 π* という.
最適政策は複数存在することもあるが,全ての最適政策は唯一のState-Value関数を共有する.
これは最適なState-Value関数 V* と呼ばれ,以下のように定義される.
V*(s) = maxπ Vπ(s), for all s ∈ S.
●最適なAction-Value関数:最適な政策はまた,
以下に示す唯一のAction-Value関数を共有する.
Q*(s,a) = max π Qπ(s,a) ,
for all s ∈ S and a ∈ A.
Q*(s,a) はQ値と呼ばれ,状態 s で行動 a を選択後,ずっと最適政策を
とりつづけるときの利得の期待値を表す.
Q*(s,a) が与えられた場合,
状態 s において最大のQ値を持つ行動 a が最適な行動である.
●Q-learningの処理手続き: S × A 個のエントリを持つ2次元配列変数Q(s,a)
を用意し,以下のように環境とのインタラクションに応じて変数を修正する。

Q-learningの処理を図式化した画像(Qlearning.jpg 88KB)
max a' Q( s',a') は,状態s'において最大のQ値を持つ行動のQ値を意味する.
● Q-learningの収束定理 [Watkins92]:
エージェントの行動選択において,全ての行動を十分な回数選択し,
かつ学習率αが Σ t = 0 ∞ α(t) → ∞
かつ Σ t = 0 ∞ α(t) 2 < ∞
を満たす時間 t の関数となっているとき,
Q-learningのアルゴリズムで得るQ値は確率1で最適なQ値に収束する(概収束).
ただし環境はエルゴート性を有する離散有限マルコフ決定過程であることを仮定する.
その他,解析については文献 [Bertsekas96]を参照.
● 行動選択方法(探査戦略):
上記の収束定理は,全ての行動を十分な回数選択しさえすれば
行動選択方法(探査戦略)には依存せずに成り立つ.
よって行動選択はランダムでもよい.
しかし,強化学習ではまだQ値が収束していない学習の途中においてもなるべく多く
の報酬を得るような行動選択を求められることが多い.
学習に応じて序々に挙動を改善していくような行動選択方法として,以下の方法が代表的である.
ネットワークのルーティングやサービス,在庫管理問題など,待ち行列を扱う
応用問題では,意志決定の時間間隔が一定ではなく,ランダムになる.
サッカーロボットのように地面を自走するロボットでは,
一定時間間隔で頻繁に意志決定すると,学習中同じ場所を行ったり来たりを
繰り返すばかりで学習が進まないため,ある行動を選択したら状態観測に
変化がみられるまで新たな意志決定をしないなどの方法がとられる[Asada97].
これらの問題では,イベントドリブンな意志決定,
つまり意志決定の時間間隔が任意な場合に対応した
強化学習が求められる.
そのような環境の数理モデルとしてセミマルコフ決定過程(SMDP)がある.
以下にSMDP環境へ対応したQ-learningアルゴリズム[Bradtke94][Parr98]を示す.

本アルゴリズムは通常のQ-learningアルゴリズムと同様の理論的性質を持つ.
探査戦略も同様.
MDPの環境では,エージェントによる環境の状態観測は完全であることが仮定さ れている. しかし実問題では,ノイズやセンサの能力が不十分なため,状態観測に不確実性 や不完全性が存在することが多い. 部分観測マルコフ決定過程(POMDP)[Lovejoy91]は,MDPのモデルを拡張し, エージェントの状態観測に不確実性を付加した数理モデルであり, 上記のような実問題をモデル化して解析する上で有用な知見を与える. POMDPの環境に対応した強化学習法は,いくつかのアプローチに分類できる [Kimura97c]:
実問題ではコントローラの状態入力が連続値のベクトルで与えられる場合が少な くない.通常のQ-learningアルゴリズムの形式に合わせて,連続値の状態入力 を適宜離散化するのが普通だが,状態入力ベクトルの次元数が大きいと「次元の 呪い(Curse of dimensionality)」と呼ばれる状態空間の爆発を招く.
連続な状態空間では,各状態間に位相構造(つまり状態間の距離を定義できる) を持つ.距離的に近い状態ではQ値も近い値を持ち,2つの状態の中間あたりに 存在する状態のQ値はそれら2つのQ値の中間くらいの値を持つことが多い. そこで,連続な状態空間を持つ強化学習問題では, Q-learningにおけるQ値やValueの表現に関数近似を用いることが多い. 関数近似を用いると,学習が高速になったり, 今まで経験したことのない状態に遭遇しても,似た状態での経験を生かして 適切な行動選択ができるなどのメリットがある. 代表的な関数近似法として,tile coding(CMAC),ニューラルネット,ファジィ, 基底関数を固定したradial-basis-function network,nearest neighbor, locally weighted linear regressionなどが提案されている[Sutton98]. 上記の関数近似は多層ニューラルネットを除いて線形アーキテクチャと呼ばれる. これは,ある状態入力 s が与えられたとき,Valueを近似するためにまず s を K 次元特徴ベクトル Φ(s) ∈ RKにマッピングし, 次に K 次元のパラメータベクトル W との線形和により V(s) = Φ(s) ・ W のように表すものである(Q値も同様). 線形アーキテクチャを用いた場合,ある条件下で最適値への収束が保証 される[Tsitsiklis97].
この他,状態空間を適応的に分割していく方法[Asada97][Moore95] なども提案されている.
実問題では連続値の状態入力と同様,連続値の行動出力を求められることも多い. 行動空間を離散化するのが普通だが,あまり粗く離散化すると細やかな制御がで きないという問題が生じる.かといって離散化が細かすぎると探索空間が増大し, 通常の離散MDPにおけるQ-learningとその行動選択方法では, なかなか学習が進まなくなり非実用的となる.
多次元の連続状態-行動空間においてQ-learningを行うための実装方法の一つとして、 筆者は「ランダムタイリングとGibbsサンプリングを用いた強化学習」を提案し, 多足ロボットシミュレータやRod-In-Maze問題,Multi-Joint Arm問題へ適用した(2005.12.06更新). ランダムタイリングは線形アーキテクチャの1つであるが, グリッドタイリングやCMACのように規則的にタイルを並べるのではなく, 空間中にランダムにタイルを配置する方法である. 不思議なことに,同数のタイルをグリッド状に規則正しく配置するよりも、 ランダムに配置したほうが遥かに良い学習結果となる。 Gibbsサンプリングとは,高次元の行動空間においてQ-learningの行動選択のために 膨大なQ値の集計を行って選択確率を行わなければならない部分を, 近似計算によって軽減するために利用した確率サンプリング法である. Gibbsサンプリング自体は, 高次元確率空間で効率良くサンプルを得るための一般的方法である. 実験では,計算コストを1万分の1程度に軽減できた. 以下に文献を示すので参考にされたし.
Fuzzy内挿型Q-learning[Horiuchi99]は, ファジィを用いた関数近似によって連続値の行動に関するQ値を表現し, 行動選択時には,行動空間を等間隔に区切ったいくつかの点についてQ値を 計算する.これらの離散的なポイントにおけるQ値を用いて行動を決定するが, 連続的な値の行動を選ぶような拡張ルーレット選択を提案している.
行動空間が連続的な場合は,Q-learningよりも
actor-critic [Sutton98][Kimura98]と
呼ばれる方法のほうが実績がある.
これは状態のValueを評価するcriticと呼ばれる部分と,状態観測に応じて
確率的に行動選択を行うactorという2つの要素より構成される.
ここでactorは行動選択の確率を調整できる物であればよい.連続値の行動
であれば,actorの確率的政策は,状態入力に応じて中心値と分散が変化す
る正規分布とする方法がある.以下に示すとおり,
行動を選択した結果,よい状態へ遷移したなら選択した行動を強化する.
正規分布のactorの場合において行動を強化するには,
実行した行動へ分布の中心値を近付け,実行した行動が標準偏差の内側なら,
正規分布の広がりを狭め,外側なら広げるよう調節すればよいので,
実装は極めて簡単である.
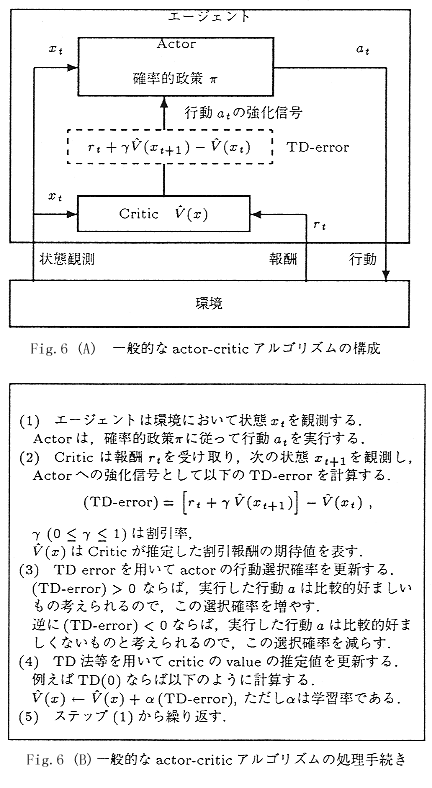
Actor-Criticの処理を図式化した画像(ActorCritic.jpg 71KB)
Criticの処理(TD法)を図式化した資料(PowerPoint2000にて作成)
・ Criticの処理(TD法)を図式化した画像(TD_method.jpg 75KB)
・ TD法がvalueを学習していく様子を図式化した画像(TDExample.jpg 71KB)
高度に複雑,巨大化したシステムでは, ある程度の機能単位ごとに自律的な知的判断部を持たせ, それらを互いに協調させる自律分散システムによる管理が求められている. これは以下の2つの理由がある.
階層的強化学習(Hierarchical RL)は,大規模な問題を分割して解くという意味 においてマルチエージェントと類似しており, 様々な方法が提案されている[Parr98][Schneider99][Wang99]. マルチエージェントと異なるのは,上位階層が下位階層(サブタスク)の知識を 再利用または共有する点と, 下位階層での部分観測性を上位階層でカバーできる点である.
画像入力など膨大なセンサからの情報からどのようにして状態表現を生成するか については,強化学習に限らずAIにおける基本的な課題である[Asada97]. また,様々なタスクを効率良く学習するためには,環境の状態遷移に関する知識 を蓄えてタスク毎に共有/再利用することが効果的と考えられる. これはモデルベース手法と呼ばれ, 多くの手法が研究されている[Kaelbling96][Sutton98]. この他,報酬の期待値最大化だけではなくリスク最小化や複数評価規範なども 研究されている.
いわゆるPHSのような通信システムでは, サービス地域をセルと呼ばれる地域に分割し,各セル内では各通話者は それぞれ異なる周波数帯を使うが,近接するセルでは同一の周波数帯を 使えないという制約がある.限られたチャンネルで可能な通話数が最大となる ように周波数を割当てることが要求される. 通話サービス要求や切断の発生は確率的で,それらの頻度はセル毎に異なる上, 動的に変動するため,大規模になると問題が極めて複雑になる. Singhらは,SMDPの強化学習に基づく方法を提案し,学習時間をさほどかけるこ となく既存のヒューリスティクスを上回る性能を達成した[Singh97].
Fig7に示すように,複数の加工機械を直列に連結して構成された
生産ラインにおいて,在庫を最小化しつつ製品の需要を満たすような最適な制御
を学習する問題である.
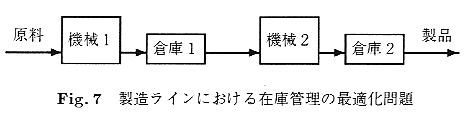
各機械の下流には倉庫(buffer)が設置され,機械の故障中あるいはメンテナンス
中の製品需要に対応することで全体の流れに与える影響を少なくする.
各機械は運用時間の増加とともに故障が発生しやすくなり,
故障すると修理が必要である.コストのかかる修理を回避し,
在庫不足によるライン停止を避け,かつ在庫もコストがかかるのでなるべく最小
限の在庫となるように,運用時間や在庫の量に応じて
機械の稼働/アイドリング/メンテナンスのタイミングを制御しなければならない.
この問題はSMDPとしてモデル化できるが,ライン全体を単一のエージェントで
学習すると問題のサイズが爆発するため,各機械毎にエージェントを割り当てる
マルチエージェントシステムが用いられている[Wang99].
トヨタのカンバン方式等と比較し,優れた制御規則を獲得したとの報告がある.
これは強化学習が状態遷移に不確実性を含み,全体の性能を最大化する問題において
強力な手法であることを示している
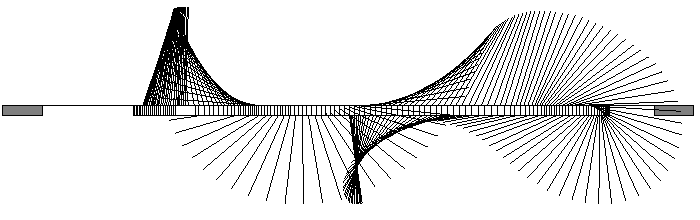
Fig.8: 倒立振子の振り上げ安定化の動作例
階層化とactor-criticに基づく連続値行動を組み合わせることで,
Fig8に示す倒立振子の振り上げ安定化をゼロから学習した
例が報告されている[Kimura99c].
政策の初期値を教師が与え,強化学習によって政策の改善を行うことにより
速やかに学習する方法も提案されている[Doya96].
エレベータ群制御,Job-Shopスケジューリング, バックギャモンやチェスなどのゲームへの適用例がある[Sutton98]. 近年では電力網の分散学習制御[Schneider99]や インターネットバナーのスケジューリングへの適用[Abe99]も報告されてい る.
本稿では強化学習を既存の問題へ適用することに重点を置き, 問題に合わせたアルゴリズムについて紹介した. しかし,実問題では強化学習で必要な「試行錯誤」が許されない場合が多く, ロボットの学習では満足な動作を獲得する前に壊れてしまうなど問題も多い. そのため,強化学習の応用に対して批判的な意見があることも事実であるが, 教師付き学習との組み合わせなどによって解決されていくものと期待される. さらに今後, 強化学習の使用を前提としたハードウエア設計がなされれば, ソフトとハードが一体となったアーキテクチャにより, 強化学習のポテンシャルを十分に生かした 今までにない新しい製品やサービスが出現する可能性がある.